Ohm’s Law: The Definitive Guide | Theory, Formulas (V=I.R), and 5 Real-World Applications
Master the fundamental principles of electricity and become an expert in circuit projects!
🔌 Did you know? Ohm's Law is one of the most important concepts in electricity and is present in virtually all electronic devices we use daily, from your smartphone to complex electrical systems.
📜 The History Behind the Law: Who was Georg Ohm?
Born in Erlangen, Germany, in 1789 (and not in 1879 as sometimes cited), Georg Simon Ohm was a brilliant physicist and mathematician whose curiosity led him to decipher one of the greatest mysteries of his time: the relationship between electrical quantities. At a time when electricity was almost magic, Ohm brought clarity and mathematics to the field.
His contribution was so monumental that the unit of electrical resistance, the Ohm (Ω), was named in his honor. Thanks to him, today we can predict, control and design circuits with incredible precision. Shall we discover his legacy together?
🧐 What is Ohm's First Law? The Simplified Concept
In essence, Ohm's First Law is the golden rule of electricity. It describes in a simple and elegant way how the three main quantities of an electrical circuit are related: Voltage, Current and Resistance.
Imagine that the law establishes an agreement between these three elements. The magical formula that expresses this relationship is:
Where each letter represents:
- V: Voltage or Potential Difference. It is the "force" that drives electrons, measured in Volts (V). Think of it as the water pressure in a faucet.
- R: Resistance. It is the opposition that the material offers to the flow of current. It is measured in Ohms (Ω). It would be like the "narrowness" of the pipe.
- I: Electric Current. It is the flow of electrons that passes through the circuit. It is measured in Amperes (A). It is equivalent to the amount of water flowing through the pipe.
The law states that, for a resistor with constant resistance, the current (I) is directly proportional to the voltage (V) applied. Doubling the voltage, you double the current. It's that simple! If you know two of these values, you can easily calculate the third.
🔑 The Best Analogy: Understanding Ohm's Law with Water
To fix this concept, nothing better than a practical analogy. Think of a simple water system:
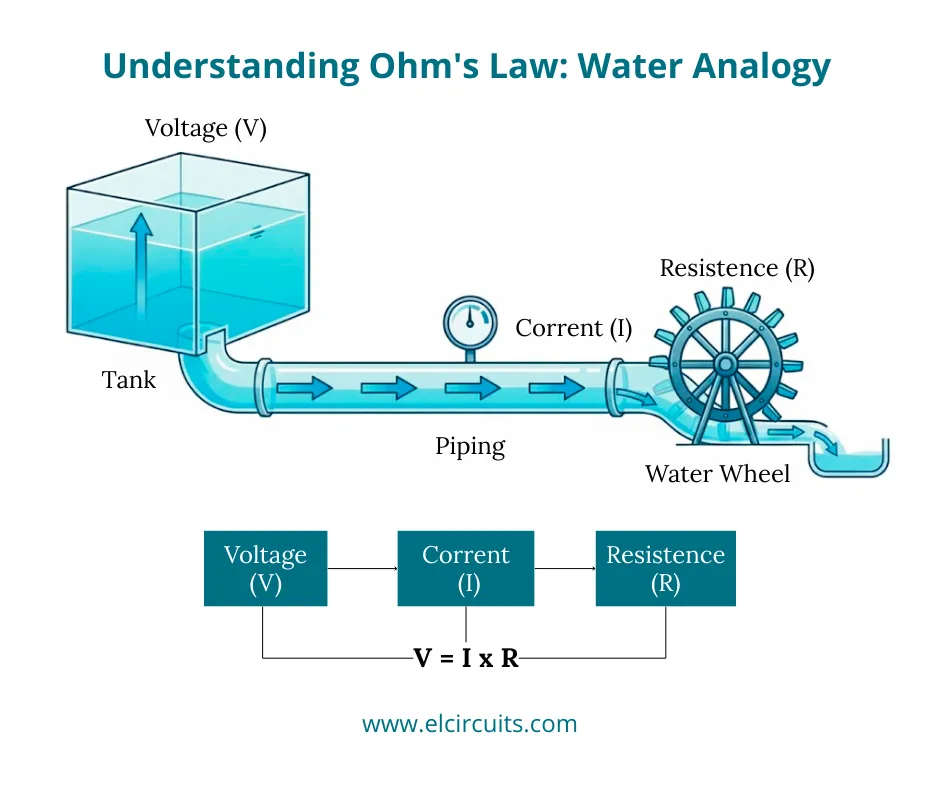
- Voltage (V) is the pressure that the water exerts in the tank. More height in the tank means more pressure.
- Current (I) is the flow of water that passes through the system per second.
- Resistance (R) is the water wheel that consumes part of the energy of the flow. A wheel with more blades or larger diameter offers more resistance to the water flow.
If you increase the water pressure (increase the Voltage), more water will flow through the system (increase the Current), making the wheel spin faster. If you maintain the pressure but increase the resistance of the wheel (more blades or larger diameter), the water flow will decrease (the Current will decrease). It's exactly how Ohm's Law works!
🧪 The Three Essential Formulas of Ohm's Law
Knowing the main formula V = R × I is great, but in practice, you'll need to calculate each of the quantities. To facilitate this, we can rearrange the equation. And to memorize, nothing better than the famous Ohm's Law Triangle.
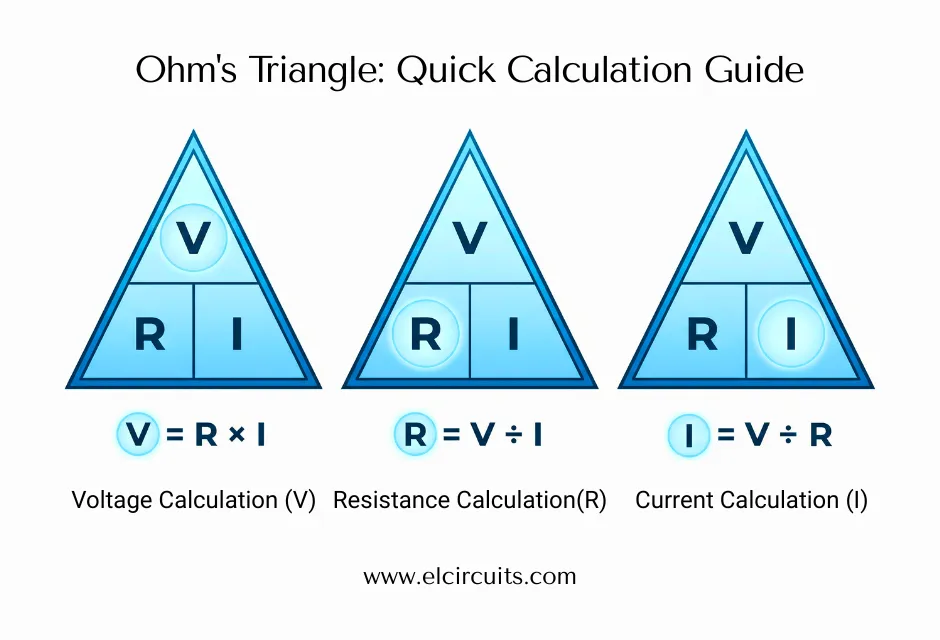
The magic happens here: cover the letter representing the Voltage (V), Resistance (R), or Current (I) you want to find in the triangle, and the position of the other two will show you the formula to use.
1️⃣ To calculate Voltage (V)
Cover the 'V' in the triangle. The 'R' and 'I' remain side by side, indicating a multiplication.
2️⃣ To calculate Current (I)
Cover the 'I'. The 'V' remains over the 'R', indicating a division.
3️⃣ To calculate Resistance (R)
Cover the 'R'. The 'V' remains over the 'I', also indicating a division.
With these three formulas at the tip of your tongue (or at your fingertips), you're ready to solve most basic electrical circuit problems!
🪛 Practical Examples: Applications of Ohm's Law in Circuits
Theory is fundamental, but practice is what solidifies knowledge. Ohm's Law is applied in countless everyday situations of an engineer, from sizing simple components to analyzing complex systems. Below, we present five practical examples that demonstrate the direct and precise application of this law in real scenarios.
🔌 Example 1 (Circuit): In a simple circuit, we have a 10 Volt source connected to a 500 Ω resistor. What is the electric current that flows through the circuit?
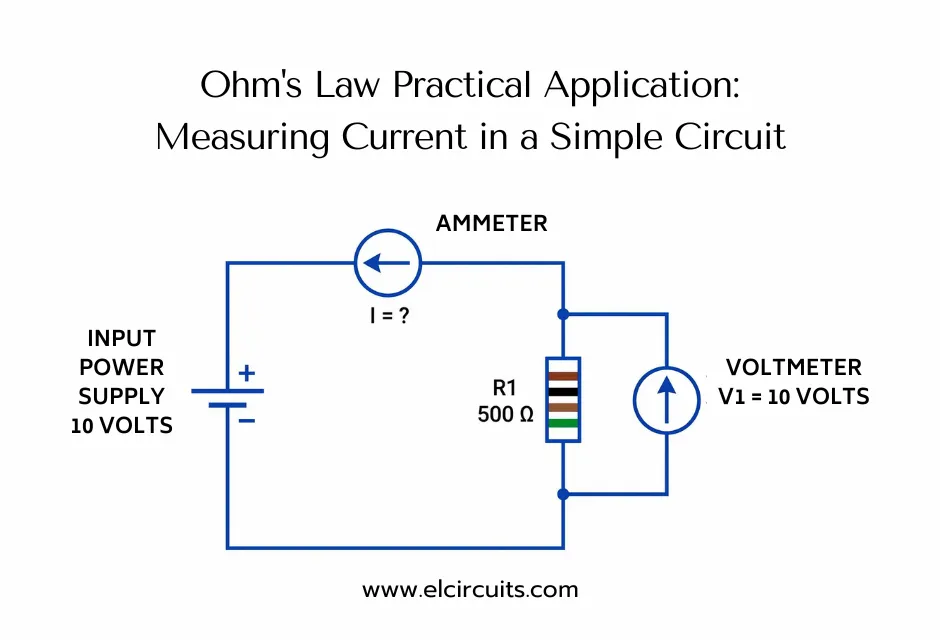
1️⃣ Step: Identify what you need to find.
The problem asks for the electric current (I).
2️⃣ Step: Identify the data you already have.
- Voltage (V) = 10 V
- Resistance (R) = 500 Ω
3️⃣ Step: Choose the correct formula.
To find the current (I), we use the formula: I = V ÷ R
4️⃣ Step: Substitute the values and calculate.
I = 0.02 A
To make it easier to read, we can convert Amperes (A) to milliamperes (mA), knowing that 1 A = 1000 mA.
Done! A current of 20 milliamperes flows through the circuit. See how simple it is?
🔴 Example 2 (LED): You want to connect an LED to a 5V source. The LED datasheet specifies a forward voltage (Vf) of 2.1V and an ideal operating current (If) of 20mA. What should be the value of the series resistor to ensure safe and efficient operation of the component?
1️⃣ Step: Identify what you need to find.
The problem asks for the value of the resistor (R).
2️⃣ Step: Identify the data you already have.
- Source voltage (Vsource) = 5 V
- LED voltage (Vf) = 2.1 V
- LED current (If) = 20 mA = 0.02 A
3️⃣ Step: Choose the correct formula.
First, we need to calculate the voltage that the resistor needs to "absorb": VR = Vsource - Vf. Then, we apply Ohm's Law to find R: R = VR ÷ If
4️⃣ Step: Substitute the values and calculate.
R = VR ÷ If = 2.9V ÷ 0.02A = 145 Ω → 150Ω (commercial value)
💡 Practical tip: Always choose the closest commercial value above the calculated one to ensure the LED lasts longer!
🏭 Example 3 (Automation): You are installing a sensor in a 24V DC industrial automation system, located 50 meters away from the source and consumes 100mA. The wiring used is a 1.5 mm² copper cable, with a resistance of approximately (0.0124 Ω/m). What is the voltage that actually reaches the sensor, considering the voltage drop in the round-trip cable?
1️⃣ Step: Identify what you need to find.
The problem asks for the voltage that reaches the sensor (Vsensor).
2️⃣ Step: Identify the data you already have.
- Source voltage (Vsource) = 24 V
- Sensor current (I) = 100 mA = 0.1 A
- Cable resistance per meter = 0.0124 Ω/m
- Cable length = 50 m (go) + 50 m (return) = 100 m
3️⃣ Step: Choose the correct formula.
First, we calculate the total resistance of the cable (Rtotal). Then, we use Ohm's Law to find the voltage drop (Vdrop) in this cable: Vdrop = I × Rtotal. Finally, we subtract this drop from the source voltage: Vsensor = Vsource - Vdrop
4️⃣ Step: Substitute the values and calculate.
Vdrop = I × Rtotal = 0.1A × 1.24Ω = 0.124V
Vsensor = Vsource - Vdrop = 24V - 0.12V = 23.876V
The voltage drop is minimal, but this calculation is crucial for higher power systems or low voltage signals, where this loss can be critical.
💡 Important alert: In real systems, drops above 5% (1.2V in 24V) can cause failures. Always calculate the voltage drop over long distances!
🤖 Example 4 (Logic Level Compatibility): You need to connect the digital output of an Arduino or PLC that operates with 5V logic to an input pin of an ESP32, which accepts a maximum of 3.3V. To protect the ESP32, you decide to use a voltage divider to reduce the signal. The divider is formed by R1 (connected to the 5V signal) and R2 (connected to GND). If you set R2 to 10 kΩ, what should be the value of R1?
1️⃣ Step: Identify what you need to find.
The problem asks for the value of the resistor R1.
2️⃣ Step: Identify the data you already have.
- Input voltage (Vin) = 5 V
- Output voltage (Vout) = 3.3 V
- Resistor R2 = 10 kΩ
3️⃣ Step: Choose the correct formula.
The voltage divider formula is: Vout = Vin × (R2 / (R1 + R2)). We need to isolate R1 in this equation.
4️⃣ Step 4: Substitute the values and calculate.
3.3 / 5 = 10kΩ / (R1 + 10kΩ)
0.66 × (R1 + 10kΩ) = 10kΩ
0.66 × R1 + 6.6kΩ = 10kΩ
0.66 × R1 = 3.4kΩ
R1 = 3.4kΩ / 0.66 ≈ 5.15 kΩ → 5.1kΩ (commercial value)
💡 Teacher's Note: This voltage divider method is a simple and effective solution for unidirectional and low speed signals (e.g., activating an input pin). For bidirectional communication (like I2C) or high-speed (SPI, UART), the professionally correct approach is to use a logic level converter module. It's safer, more robust, and guarantees data integrity.
🔋 Example 5 (Battery): You tested a battery: without load, the voltage at its terminals is 12.6V, but when connecting a load of 2A, the voltage at the terminals drops to 12.1V. What is the internal resistance (Rint) of the battery?
1️⃣ Step: Identify what you need to find.
The problem asks for the internal resistance of the battery (Rint).
2️⃣ Step: Identify the data you already have.
- No-load voltage (Vno load) = 12.6 V
- Load voltage (Vwith load) = 12.1 V
- Load current (I) = 2 A
3️⃣ Step: Choose the correct formula.
The voltage drop in the battery is caused by its own internal resistance. This drop (ΔV) is proportional to the current that passes through it, according to Ohm's Law: ΔV = I × Rint, where ΔV = Vno load - Vwith load.
4️⃣ Step: Substitute the values and calculate.
Rint = ΔV / I = 0.5V / 2A = 0.25 Ω
💡 Teacher's tip: Batteries with internal resistance above 0.5Ω are worn out and don't deliver enough power for starting or heavy loads.
🤔 Frequently Asked Questions (FAQ)
To ensure your project is a success, we've compiled some of the most common questions about Ohm's Law. Check them out!
Does Ohm's Law apply to all electronic components? 🔽
No. Ohm's Law applies perfectly to "ohmic" components, such as most metal resistors. However, components like diodes, transistors, and incandescent lamps have a resistance that varies with voltage or temperature, and therefore do not follow a linear relationship.
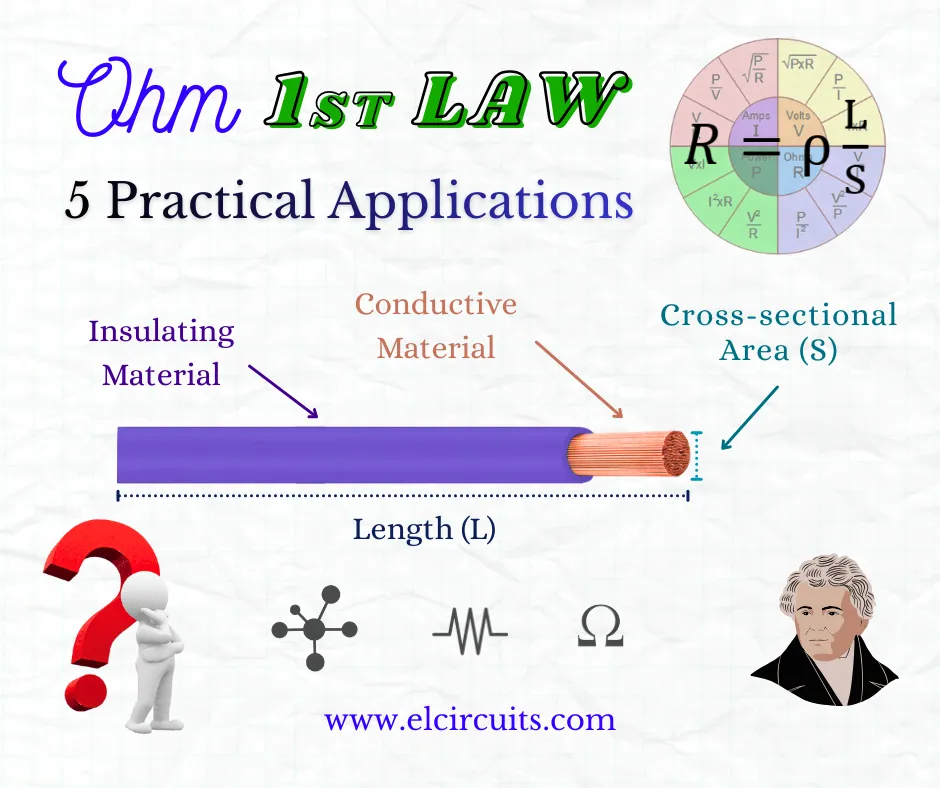
What is the difference between Ohm's First and Second Law? 🔽
The First Law (V=R×I) describes the relationship between voltage, current, and resistance at a point in the circuit. The Second Law (R = ρ × L / A) calculates the resistance of a material based on its physical properties: the resistivity of the material (ρ), the length (L), and the cross-sectional area (A).
Why is Ohm's Law so important? 🔽
It's the foundation for the analysis, design, and diagnosis of virtually all electrical and electronic circuits. Without it, it would be impossible to calculate the current in a circuit, size a resistor to protect an LED, or understand the voltage drop in a wire.
🧾 Conclusion: The Key to the World of Electricity
Ohm's First Law is much more than a simple formula; it's the fundamental language that describes how electricity behaves. Understanding V = R × I gives you the power to predict, control, and innovate in the world of electronics.
Whether you're a student starting your journey, a professional looking to refresh your memory, or a hobbyist working on your next project, mastering Ohm's Law is the first and most crucial step to success.
✨ Our Gratitude and Next Steps
We sincerely hope this guide has been useful and enriching for your projects! Thank you for dedicating your time to this content.
Your Feedback is Invaluable:
Have any questions, suggestions, or corrections? Feel free to share them in the comments below! Your contribution helps us refine this content for the entire ElCircuits community.
If you found this guide helpful, spread the knowledge!
🔗 Share This GuideBest regards,
The ElCircuits Team ⚡
 Português
Português Español
Español